
Automatic calibration of conceptual rainfall-runoff models: sensitivity to calibration data. The missing values in obs and sim are removed before the computation proceeds, and only those positions with non-missing values in obs and sim are considered in the computation Author(s) Obs and sim has to have the same length/dimension If sim and obs are matrixes, the returned value is a vector, with the mean squared error between each column of sim and obs. Root mean square error or root mean square deviation is one of the most commonly used measures for evaluating the quality of predictions. Mse = mean( (sim - obs)^2, na.rm = TRUE) Value When an 'NA' value is found at the i-th position in obs OR sim, the i-th value of obs AND sim are removed before the computation.įurther arguments passed to or from other methods.

Numeric, zoo, matrix or ame with observed valuesĪ logical value indicating whether 'NA' should be stripped before the computation proceeds. Numeric, zoo, matrix or ame with simulated values

) # S3 method for class 'zoo' mse ( sim, obs, na.rm = TRUE. ) # S3 method for class 'matrix' mse ( sim, obs, na.rm = TRUE. ) # S3 method for class 'ame' mse ( sim, obs, na.rm = TRUE. ) # Default S3 method: mse ( sim, obs, na.rm = TRUE.

hydroGOF-internal: Internal hydroGOF objects.It can be used as the measure of the quality of an. It measures the average squared difference between the estimator and the parameter. Mean squared error gives the mean of squared difference between model prediction and target value. gof: Numerical Goodness-of-fit measures The mean squared error is a measure of performance of a point estimator.EgaEnEstellaQts: Ega in "Estella" (Q071), ts with daily streamflows.Read on to know how the mean squared error measures how close a regression line is to a set of. Through this demonstration, we hope to show that each component in a decomposition represents a distinct concept, like “season” or “variability,” and that simple decompositions can be combined to represent more complex concepts, like “seasonal variability,” creating an expressive language through which to interrogate models and data. Check out the comprehensive guide to understand mean squared error. To demonstrate the versatility of this approach, we outline some fundamental types of decomposition and apply them to predictions at 1,021 streamgages across the conterminous United States from three streamflow models.
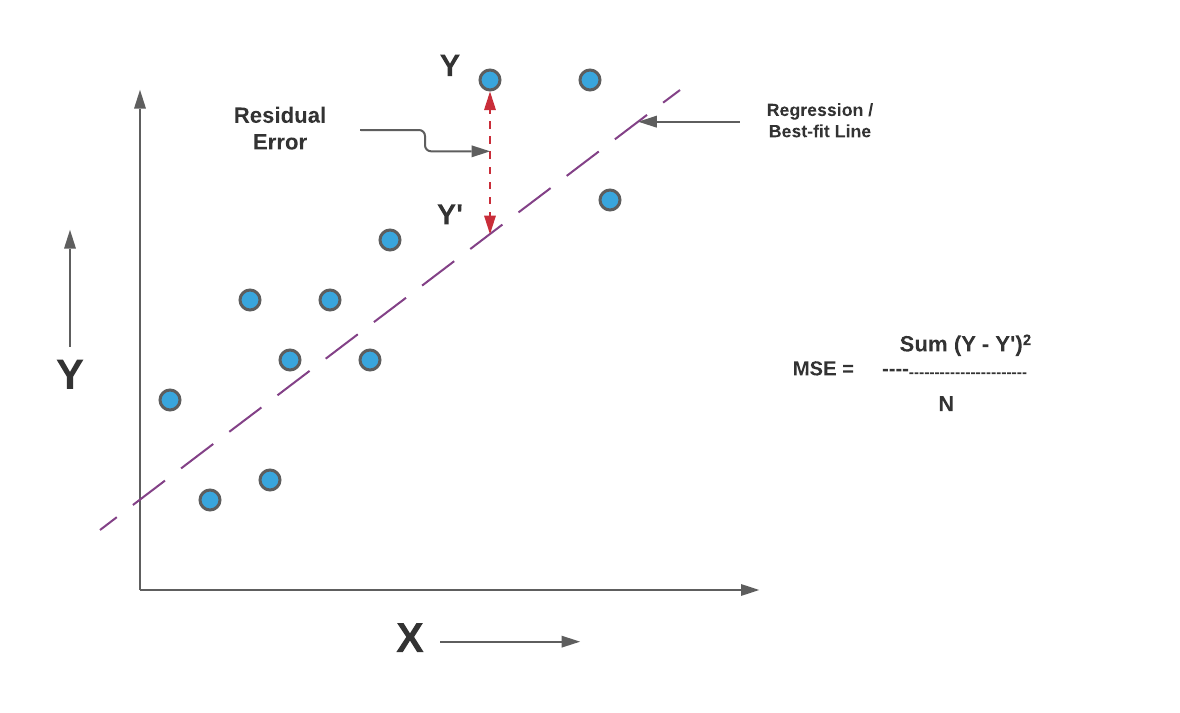
The loss is the mean overseen data of the squared differences between true and. After computing the squared distance between the inputs, the mean value over the last dimension. We contend that, a better approach to model benchmarking and interpretation is to decompose MSE into interpretable components. Mean squared error (MSE) is the most commonly used loss function for regression. Computes the mean squared error between labels and predictions. Such scores are inherently subjective, however, and while their components may be interpretable, the composite itself is not. For normally distributed data, mean squared error (MSE) is ideal as an objective measure of model performance, but it gives little insight into what aspects of model performance are “good” or “bad.” This apparent weakness has led to a myriad of specialized error metrics, which are sometimes aggregated to form a composite score. As science becomes increasingly cross-disciplinary and scientific models become increasingly cross-coupled, standardized practices of model evaluation are more important than ever.


 0 kommentar(er)
0 kommentar(er)
